vnpy/docs/cta_backtester.md

# CTA回测模块
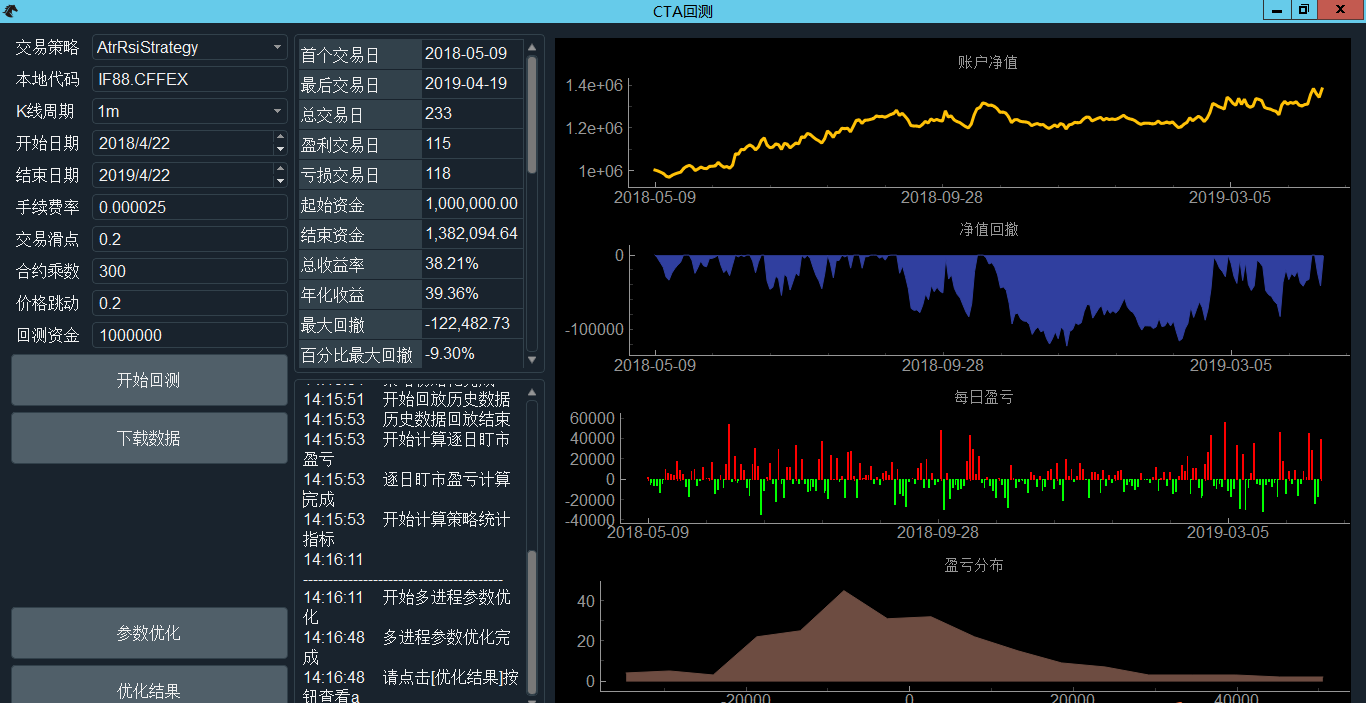
CTA回测模块是基于PyQt5和pyqtgraph的图形化回测工具。启动VN Trader后，在菜单栏中点击“功能-> CTA回测”即可进入该图形化回测界面，如下图。CTA回测模块主要实现3个功能：历史行情数据的下载、策略回测、参数优化。

![](https://vnpy-community.oss-cn-shanghai.aliyuncs.com/forum_experience/yazhang/cta_backtester/cta_backtester.png)

 

## 加载启动
进入图形化回测界面“CTA回测”后，会立刻完成初始化工作：初始化回测引擎、初始化RQData客户端。

```
    def init_engine(self):
        """"""
        self.write_log("初始化CTA回测引擎")

        self.backtesting_engine = BacktestingEngine()
        # Redirect log from backtesting engine outside.
        self.backtesting_engine.output = self.write_log

        self.write_log("策略文件加载完成")

        self.init_rqdata()

    def init_rqdata(self):
        """
        Init RQData client.
        """
        result = rqdata_client.init()
        if result:
            self.write_log("RQData数据接口初始化成功")
```

 


## 下载数据
在开始策略回测之前，必须保证数据库内有充足的历史数据。故vnpy提供了历史数据一键下载的功能。
下载数据功能主要是基于RQData的get_price()函数实现的。
```
get_price(
    order_book_ids, start_date='2013-01-04', end_date='2014-01-04',
    frequency='1d', fields=None, adjust_type='pre', skip_suspended =False,
    market='cn'
)
```


在使用前要保证RQData初始化完毕，然后填写以下4个字段信息：
- 本地代码：格式为合约品种+交易所，如IF88.CFFEX、rb88.SHFE；然后在底层通过RqdataClient的to_rq_symbol()函数转换成符合RQData格式，对应RQData中get_price()函数的order_book_ids字段。
- K线周期：可以填1m、60m、1d，对应get_price()函数的frequency字段。
- 开始日期：格式为yy/mm/dd，如2017/4/21，对应get_price()函数的start_date字段。（点击窗口右侧箭头按钮可改变日期大小）
- 结束日期：格式为yy/mm/dd，如2019/4/22，对应get_price()函数的end_date字段。（点击窗口右侧箭头按钮可改变日期大小）
  
填写完字段信息后，点击下方“下载数据”按钮启动下载程序，下载成功如图所示。


![](https://vnpy-community.oss-cn-shanghai.aliyuncs.com/forum_experience/yazhang/cta_backtester/data_loader.png)



 

## 策略回测
下载完历史数据后，需要配置以下字段：交易策略、手续费率、交易滑点、合约乘数、价格跳动、回测资金。
这些字段主要对应BacktesterEngine类的run_backtesting函数。
```
def run_backtesting(
    self, class_name: str, vt_symbol: str, interval: str, start: datetime, 
    end: datetime, rate: float, slippage: float, size: int, pricetick: float, 
    capital: int, setting: dict
)：
```

点击下方的“开始回测”按钮可以开始回测：
首先会弹出如图所示的参数配置窗口，用于调整策略参数。该设置对应的是run_backtesting()函数的setting字典。

![](https://vnpy-community.oss-cn-shanghai.aliyuncs.com/forum_experience/yazhang/cta_backtester/parameter_setting.png)



点击“确认”按钮后开始运行回测，同时日志界面会输出相关信息，如图。

![](https://vnpy-community.oss-cn-shanghai.aliyuncs.com/forum_experience/yazhang/cta_backtester/backtesting_log.png)

回测完成后会显示统计数字图表。

 

### 统计数据
用于显示回测完成后的相关统计数值, 如结束资金、总收益率、夏普比率、收益回撤比。

![](https://vnpy-community.oss-cn-shanghai.aliyuncs.com/forum_experience/yazhang/cta_backtester/show_result.png)

 

### 图表分析
以下四个图分别是代表账号净值、净值回撤、每日盈亏、盈亏分布。

![](https://vnpy-community.oss-cn-shanghai.aliyuncs.com/forum_experience/yazhang/cta_backtester/show_result_chat.png)


 

## 参数优化
vnpy提供2种参数优化的解决方案：穷举算法、遗传算法


 

### 穷举算法

穷举算法原理：
- 输入需要优化的参数名、优化区间、优化步进，以及优化目标。
```
    def add_parameter(
        self, name: str, start: float, end: float = None, step: float = None
    ):
        """"""
        if not end and not step:
            self.params[name] = [start]
            return

        if start >= end:
            print("参数优化起始点必须小于终止点")
            return

        if step <= 0:
            print("参数优化步进必须大于0")
            return

        value = start
        value_list = []

        while value <= end:
            value_list.append(value)
            value += step

        self.params[name] = value_list

    def set_target(self, target_name: str):
        """"""
        self.target_name = target_name
```

&nbsp;


- 形成全局参数组合, 数据结构为[{key: value, key: value}, {key: value, key: value}]。
```
    def generate_setting(self):
        """"""
        keys = self.params.keys()
        values = self.params.values()
        products = list(product(*values))

        settings = []
        for p in products:
            setting = dict(zip(keys, p))
            settings.append(setting)

        return settings
```
&nbsp;


- 遍历全局中的每一个参数组合：遍历的过程即运行一次策略回测，并且返回优化目标数值；然后根据目标数值排序，输出优化结果。
```
    def run_optimization(self, optimization_setting: OptimizationSetting, output=True):
        """"""
        # Get optimization setting and target
        settings = optimization_setting.generate_setting()
        target_name = optimization_setting.target_name

        if not settings:
            self.output("优化参数组合为空，请检查")
            return

        if not target_name:
            self.output("优化目标未设置，请检查")
            return

        # Use multiprocessing pool for running backtesting with different setting
        pool = multiprocessing.Pool(multiprocessing.cpu_count())

        results = []
        for setting in settings:
            result = (pool.apply_async(optimize, (
                target_name,
                self.strategy_class,
                setting,
                self.vt_symbol,
                self.interval,
                self.start,
                self.rate,
                self.slippage,
                self.size,
                self.pricetick,
                self.capital,
                self.end,
                self.mode
            )))
            results.append(result)

        pool.close()
        pool.join()

        # Sort results and output
        result_values = [result.get() for result in results]
        result_values.sort(reverse=True, key=lambda result: result[1])

        if output:
            for value in result_values:
                msg = f"参数：{value[0]}, 目标：{value[1]}"
                self.output(msg)

        return result_values
```




注意：可以使用multiprocessing库来创建多进程实现并行优化。例如：若用户计算机是2核，优化时间为原来1/2；若计算机是10核，优化时间为原来1/10。

&nbsp;


穷举算法操作：

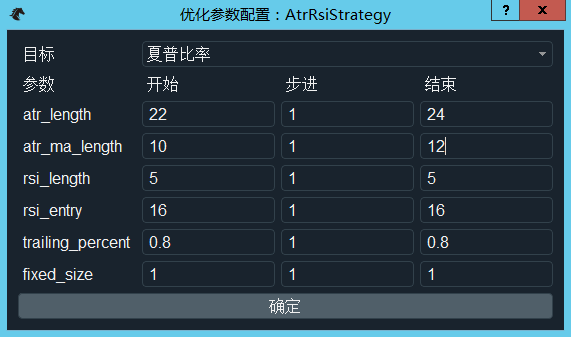
- 点击“参数优化”按钮，会弹出“优化参数配置”窗口，用于设置优化目标（如最大化夏普比率、最大化收益回撤比）和设置需要优化的参数以及优化区间，如图。
  
![](https://vnpy-community.oss-cn-shanghai.aliyuncs.com/forum_experience/yazhang/cta_backtester/optimize_setting.png)

- 设置好需要优化的参数后，点击“优化参数配置”窗口下方的“确认”按钮开始进行调用CPU多核进行多进程并行优化，同时日志会输出相关信息。
  
![](https://vnpy-community.oss-cn-shanghai.aliyuncs.com/forum_experience/yazhang/cta_backtester/optimize_log.png)

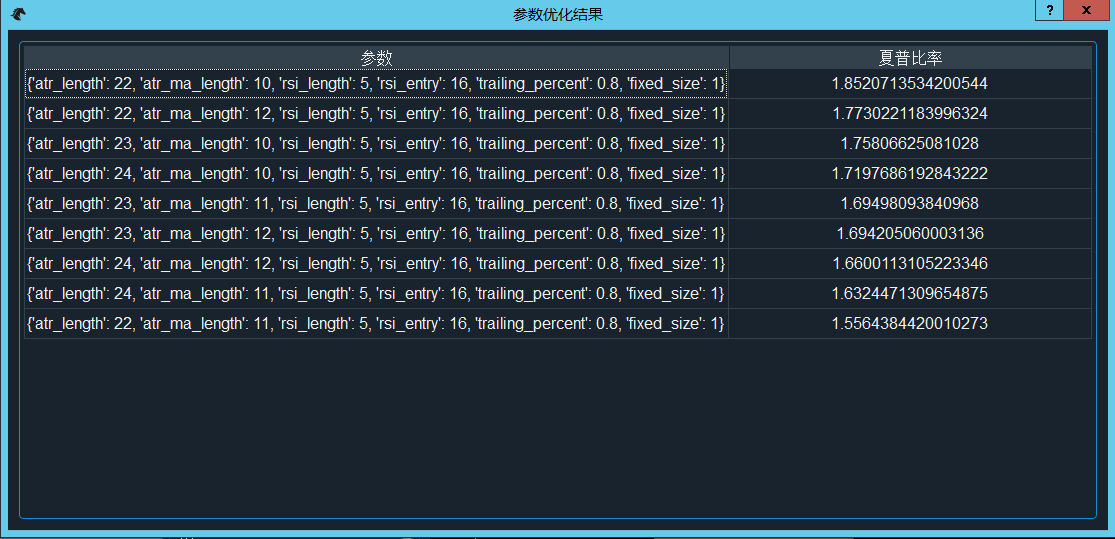
- 点击“优化结果”按钮可以看出优化结果，如图的参数组合是基于目标数值（夏普比率）由高到低的顺序排列的。
  
![](https://vnpy-community.oss-cn-shanghai.aliyuncs.com/forum_experience/yazhang/cta_backtester/optimize_result.png)


&nbsp;

### 遗传算法

遗传算法原理：

- 输入需要优化的参数名、优化区间、优化步进，以及优化目标；

- 形成全局参数组合，该组合的数据结构是列表内镶嵌元组，即[[(key, value), (key, value)] , [(key, value), (key,value)]]，与穷举算法的全局参数组合的数据结构不同。这样做的目的是有利于参数间进行交叉互换和变异。
```
    def generate_setting_ga(self):
        """""" 
        settings_ga = []
        settings = self.generate_setting()     
        for d in settings:            
            param = [tuple(i) for i in d.items()]
            settings_ga.append(param)
        return settings_ga
```

&nbsp;


- 形成个体：调用random()函数随机从全局参数组合中获取参数。
```
        def generate_parameter():
            """"""
            return random.choice(settings)
```

&nbsp;


- 定义个体变异规则: 即发生变异时，旧的个体完全被新的个体替代。
```
        def mutate_individual(individual, indpb):
            """"""
            size = len(individual)
            paramlist = generate_parameter()
            for i in range(size):
                if random.random() < indpb:
                    individual[i] = paramlist[i]
            return individual,
```

&nbsp;


- 定义评估函数：入参的是个体，即[(key, value), (key, value)]形式的参数组合，然后通过dict()转化成setting字典，然后运行回测，输出目标优化数值，如夏普比率、收益回撤比。(注意，修饰器@lru_cache作用是缓存计算结果，避免遇到相同的输入重复计算，大大降低运行遗传算法的时间)
```
@lru_cache(maxsize=1000000)
def _ga_optimize(parameter_values: tuple):
    """"""
    setting = dict(parameter_values)

    result = optimize(
        ga_target_name,
        ga_strategy_class,
        setting,
        ga_vt_symbol,
        ga_interval,
        ga_start,
        ga_rate,
        ga_slippage,
        ga_size,
        ga_pricetick,
        ga_capital,
        ga_end,
        ga_mode
    )
    return (result[1],)


def ga_optimize(parameter_values: list):
    """"""
    return _ga_optimize(tuple(parameter_values))
```

&nbsp;

- 运行遗传算法：调用deap库的算法引擎来运行遗传算法，其具体流程如下。
1）先定义优化方向，如夏普比率最大化；
2）然后随机从全局参数组合获取个体，并形成族群；
3）对族群内所有个体进行评估（即运行回测），并且剔除表现不好个体；
4）剩下的个体会进行交叉或者变异，通过评估和筛选后形成新的族群；（到此为止是完整的一次种群迭代过程）；
5）多次迭代后，种群内差异性减少，整体适应性提高，最终输出建议结果。该结果为帕累托解集，可以是1个或者多个参数组合。

注意：由于用到了@lru_cache, 迭代中后期的速度回提高非常多，因为很多重复的输入都避免了再次的回测，直接在内存中查询并且返回计算结果。
```
from deap import creator, base, tools, algorithms
creator.create("FitnessMax", base.Fitness, weights=(1.0,))
creator.create("Individual", list, fitness=creator.FitnessMax)
        ......
        # Set up genetic algorithem
        toolbox = base.Toolbox() 
        toolbox.register("individual", tools.initIterate, creator.Individual, generate_parameter)                          
        toolbox.register("population", tools.initRepeat, list, toolbox.individual)                                            
        toolbox.register("mate", tools.cxTwoPoint)                                               
        toolbox.register("mutate", mutate_individual, indpb=1)               
        toolbox.register("evaluate", ga_optimize)                                                
        toolbox.register("select", tools.selNSGA2)       

        total_size = len(settings)
        pop_size = population_size                      # number of individuals in each generation
        lambda_ = pop_size                              # number of children to produce at each generation
        mu = int(pop_size * 0.8)                        # number of individuals to select for the next generation

        cxpb = 0.95         # probability that an offspring is produced by crossover    
        mutpb = 1 - cxpb    # probability that an offspring is produced by mutation
        ngen = ngen_size    # number of generation
                
        pop = toolbox.population(pop_size)      
        hof = tools.ParetoFront()               # end result of pareto front

        stats = tools.Statistics(lambda ind: ind.fitness.values)
        np.set_printoptions(suppress=True)
        stats.register("mean", np.mean, axis=0)
        stats.register("std", np.std, axis=0)
        stats.register("min", np.min, axis=0)
        stats.register("max", np.max, axis=0)

        algorithms.eaMuPlusLambda(
            pop, 
            toolbox, 
            mu, 
            lambda_, 
            cxpb, 
            mutpb, 
            ngen, 
            stats,
            halloffame=hof
        )

        # Return result list
        results = []

        for parameter_values in hof:
            setting = dict(parameter_values)
            target_value = ga_optimize(parameter_values)[0]
            results.append((setting, target_value, {}))
        
        return results
```